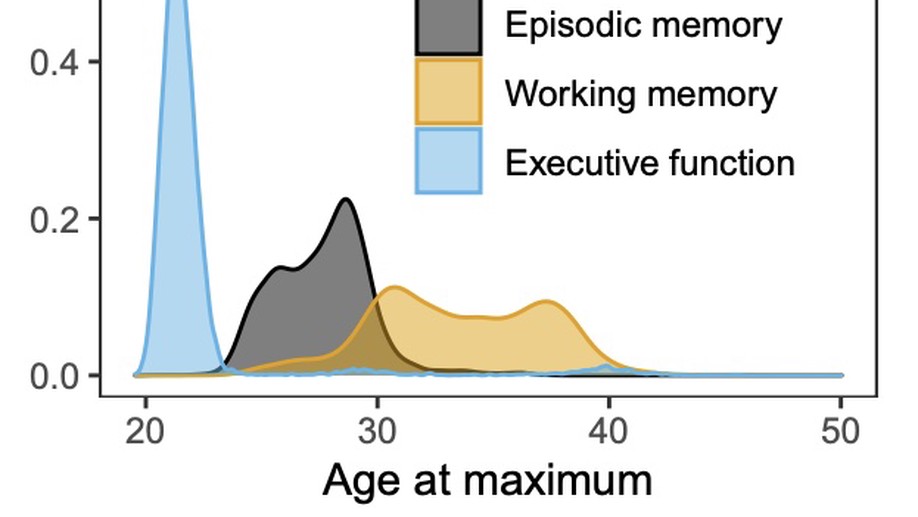
Longitudinal modeling of age-dependent latent traits with generalized additive latent and mixed models
We present generalized additive latent and mixed models (GALAMMs) for analysis of clustered data with responses and latent variables depending smoothly on observed variables. A scalable maximum likelihood estimation algorithm is proposed, utilizing the Laplace approximation, sparse matrix computation, and automatic differentiation. Mixed response types, heteroscedasticity, and crossed random effects are naturally incorporated into the framework. The models developed were motivated by applications in cognitive neuroscience, and two case studies are presented.
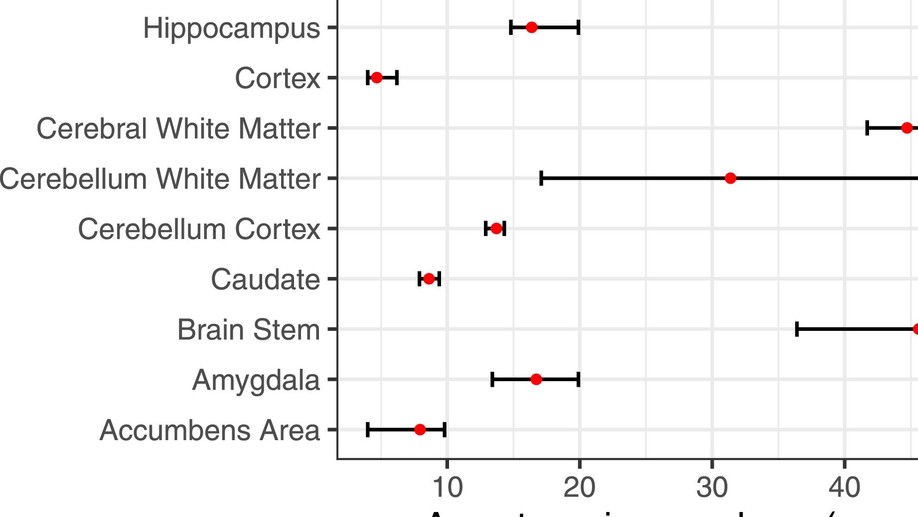
A recipe for accurate estimation of lifespan brain trajectories, distinguishing longitudinal and cohort effects
We address the problem of estimating how different parts of the brain develop and change throughout the lifespan, and how these trajectories are affected by genetic and environmental factors. Estimation of these lifespan trajectories is statistically challenging, since their shapes are typically highly nonlinear, and although true change can only be quantified by longitudinal examinations, as follow-up intervals in neuroimaging studies typically cover less than 10% of the lifespan, use of cross-sectional information is necessary.
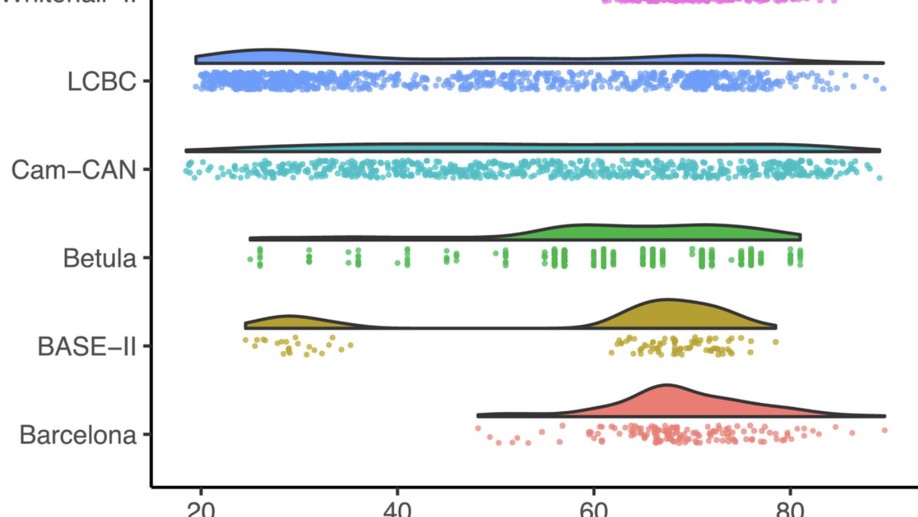
Meta-analysis of generalized additive models in neuroimaging studies
Analyzing data from multiple neuroimaging studies has great potential in terms of increasing statistical power, enabling detection of effects of smaller magnitude than would be possible when analyzing each study separately and also allowing to systematically investigate between-study differences. Restrictions due to privacy or proprietary data as well as more practical concerns can make it hard to share neuroimaging datasets, such that analyzing all data in a common location might be impractical or impossible.
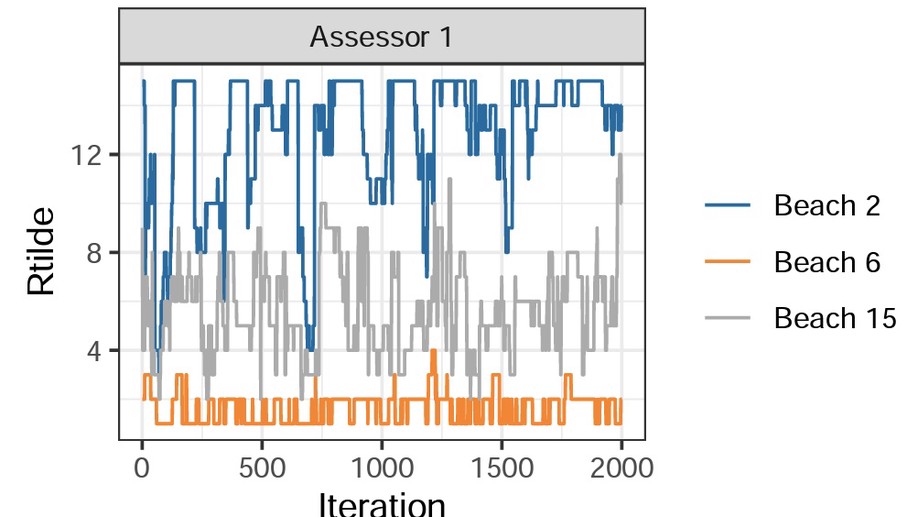
BayesMallows: An R Package for the Bayesian Mallows Model
BayesMallows is an R package for analyzing preference data in the form of rankings with the Mallows rank model, and its finite mixture extension, in a Bayesian framework. The model is grounded on the idea that the probability density of an observed ranking decreases exponentially with the distance to the location parameter. It is the first Bayesian implementation that allows wide choices of distances, and it works well with a large amount of items to be ranked.
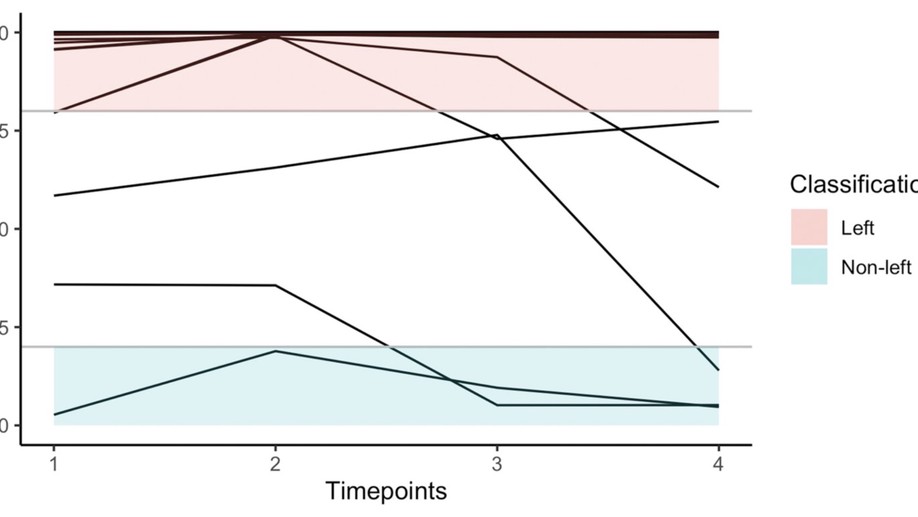
From observed laterality to latent hemispheric differences: Revisiting the inference problem
Researchers interested in hemispheric dominance frequently aim to infer latent functional differences between the hemispheres from observed lateral behavioural or brain-activation differences. To be valid, these inferences may not only rely on the observed laterality measures but also need to account for the antecedent probabilities of the studied latent classes. This fact is frequently ignored in the literature, leading to misclassifications especially when considering low probability classes as, for example, “atypical” right hemispheric language dominance.

hdme: High-Dimensional Regression with Measurement Error
This is the companion paper to the hdme R package. Link to paper.

Probabilistic preference learning with the Mallows rank model
Ranking and comparing items is crucial for collecting information about preferences in many areas, from marketing to politics. The Mallows rank model is among the most successful approaches to analyze rank data, but its computational complexity has limited its use to a particular form based on Kendall distance. We develop new computationally tractable methods for Bayesian inference in Mallows models that work with any right-invariant distance. Our method performs inference on the consensus ranking of the items, also when based on partial rankings, such as top-k items or pairwise comparisons.

Covariate Selection in High-Dimensional Generalized Linear Models With Measurement Error
In many problems involving generalized linear models, the covariates are subject to measurement error. When the number of covariates p exceeds the sample size n, regularized methods like the lasso or Dantzig selector are required. Several recent papers have studied methods which correct for measurement error in the lasso or Dantzig selector for linear models in the p > n setting. We study a correction for generalized linear models, based on Rosenbaum and Tsybakov’s matrix uncertainty selector.
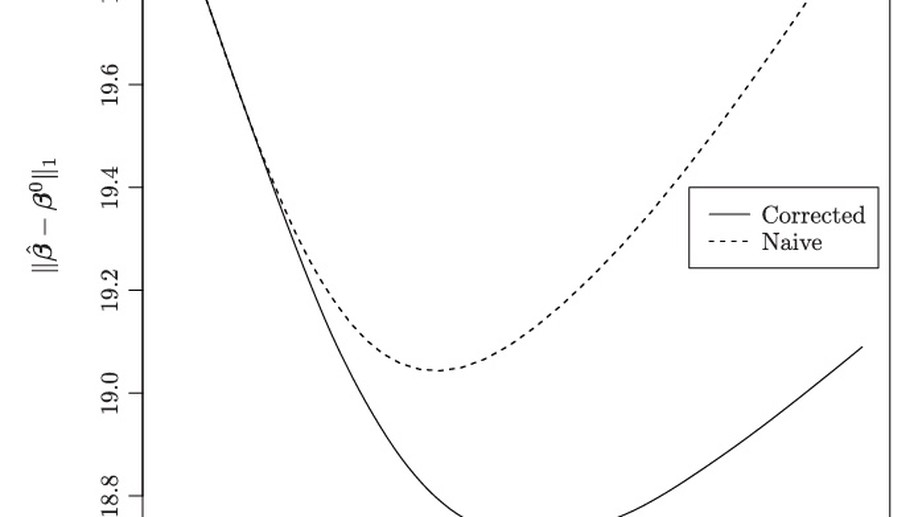
Measurement error in Lasso: Impact and likelihood bias correction
Regression with the lasso penalty is a popular tool for performing dimension reduction when the number of covariates is large. In many applications of the lasso, like in genomics, covariates are subject to measurement error. We study the impact of measurement error on linear regression with the lasso penalty, both analytically and in simulation experiments. A simple method of correction for measurement error in the lasso is then considered. In the large sample limit, the corrected lasso yields sign consistent covariate selection under conditions very similar to the lasso with perfect measurements, whereas the uncorrected lasso requires much more stringent conditions on the covariance structure of the data.